Harry Geels: Het gemiddelde is een denkfout
Harry Geels: Het gemiddelde is een denkfout

Door Harry Geels
Vorig jaar ontspon zich op Twitter een discussie tussen bekende wetenschappers over de zwakte van veel empirische studies die ‘gemiddelden’ als richtlijn geven. Om de kracht van samengestelde interest of beleggen in aandelen op de lange termijn aan te tonen, worden bijvoorbeeld vaak gemiddelden aangehaald. Het gemiddelde is voor de financiële wereld echter meestal een denkfout.
Als het om beleggen gaat, wordt vaak gebruikt gemaakt van gemiddelden. Zo zouden aandelen, afhankelijk van de beurs, gemiddeld 8% per jaar opleveren, of zou de gemiddelde koers-winstverhouding van Amerikaanse aandelen, bij een rentestand van tussen de 3,2 en 3,8%, 17 zijn. Gemiddelden kunnen echter een vertekend beeld geven.
Het meest gebruikte voorbeeld om aan te tonen dat we moeten beleggen in aandelen voor de lange termijn is onderstaand plaatje, waarbij met behulp van samengesteld rendement (compounded returns) van 8% per jaar een mooi plaatje voor de langetermijnbelegger in het vooruitzicht wordt gesteld. Iemand die begint met beleggen en de eerste tien jaar $12k per jaar inlegt, zou over veertig jaar $2,6 miljoen bezitten. Dit geeft een vertekend beeld, omdat aandelen niet ieder jaar 8% stijgen.
Figuur 1: De kracht van samengeteld rendement (10 jaar $12k beleggen tegen 8% gemiddeld per jaar)
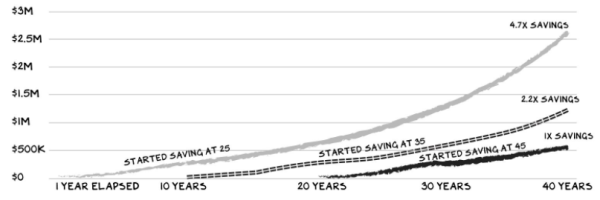
Bron: Prof G. Analysis
Nog een willekeurig voorbeeld van werken met gemiddelden: recent kwam Robert J. Shiller met een nieuwe, reeds veelbesproken studie waarin werd aangetoond dat de hoogste waarderingen van Amerikaanse aandelen niet plaatsvinden als de rente het laagst staat, maar juist in een klimaat waarin de rente wat hoger staat. Zie ook figuur 2.
Het grote probleem van een dergelijk plaatje is dat de gemiddelde koers-winstverhoudingen bij verschillende ‘interest rate buckets’ erg door bepaalde, meestal unieke perioden kunnen zijn beïnvloed.
Figuur 2: Gemiddelde koers/winst-ratio’s in verschillende renteklimaten; Amerikaanse aandelen, periode 1872-2020
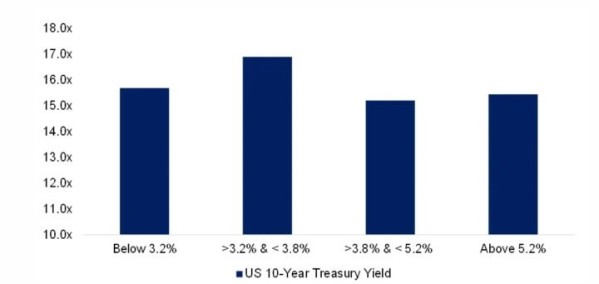
Bron: Robert J. Shiller Library, FactorResearch
Kortom, we hebben het over de denkfout van het gemiddelde, in het Engels ‘the fallacy of the average’. Een niet-goede zwemmer kan bij het oversteken verdrinken in een rivier die gemiddeld 50 cm diep is, omdat die toch ergens, zij het maar over een korte afstand, bijvoorbeeld vier meter diep is. Even kort door de bocht: hoe meer rendementen ‘skewed’ zijn, of staartrisico (‘kurtosis’) hebben, hoe minder goed gemiddelden werken.
Ergodiciteit
Eind vorig jaar pakte Bloomberg een discussie op tussen diverse risicomanagement- en beleggingsexperts, over een studie van Ole Peters, een natuurkundige, die kort door de bocht stelt dat alles wat we van de Moderne Portefeuille Theorie hebben geleerd, fout is. Meer specifiek viel Peters de Nutsfunctie aan die stelt dat je in ‘iets’ moet beleggen als het verwachte rendement groter is dan de voor de risicotolerantie gecorrigeerde volatiliteit (risico).
Peters kreeg, via Twitter, bijval van onder andere Nassim Taleb en Michael Mauboussin. De kern van de zaak draait om het begrip ‘ergodiciteit’, ofwel dat het gemiddelde van de mogelijke uitkomsten van een gegeven situatie iemand, in ons geval de belegger, informeert over hoe hij iets ervaart (of hoe hij gaat handelen). Dit concept heeft vergaande gevolgen voor alle geledingen in de financiële wereld, van risicomanagers tot monetaire autoriteiten en beleggers.
Experimenten als bewijs
Om het standpunt van Peters gemakkelijk duidelijk te maken, volstaat een experiment. Stel we beginnen met $100 en we krijgen 50% positief rendement uitgekeerd bij kop en 40% verlies voor de kiezen bij munt. Het gemiddelde is positief, namelijk 5% (50%-40%/2). Toch is 50% winst (bij kop) en 40% verlies (bij munt) een verliesgevend ‘spel’ (tenminste, met een eerlijke munt waarbij de kans op kop en munt even groot is).
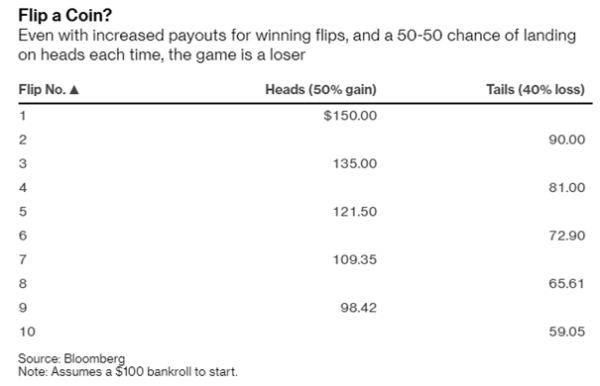
De bovenstaande tabel laat zien dat na precies vijf keer munt en vijf keer kop gooien (om-en-om) er van de $100 startwaarde nog maar $59,05 over is. Omdat er ook andere iteraties mogelijk zijn laat onderstaande figuur zien dat er ook in alternatieve reeksen verliezen zijn, behalve dan bij steeds kop gooien (iemand die in dat laatste zou slagen, wordt in de financiële wereld nog weleens een expert of goeroe genoemd, maar dat terzijde). Het figuurtje rechtsboven komt overeen met bovenstaande tabel.
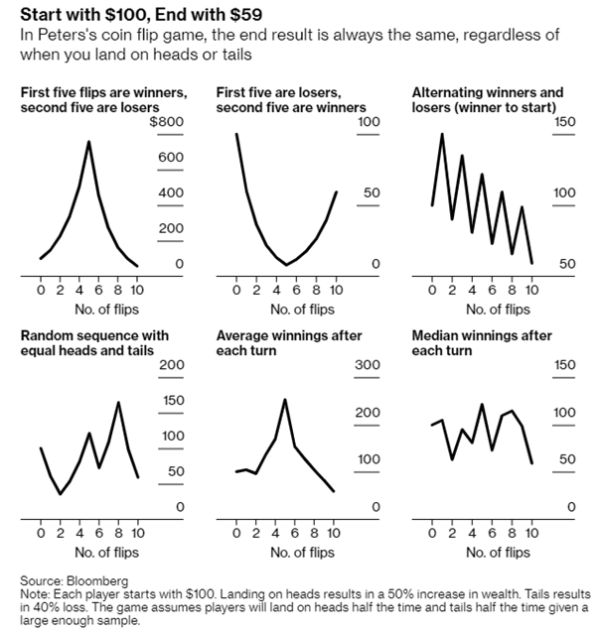
Taleb stelt naar aanleiding van de studie van Peters: ‘Het begrip nut mag bestaan, maar niet op de manier waarop economen het hebben gemodelleerd. De meest gebruikte modellen zijn monsterlijk fout.’
‘Volatility kills the cat’
Een van de grote problemen is wat we ‘variance drain’ of ‘volatility drag’ noemen: hoe volatieler de rendementen zijn, hoe meer het rendement door de tijd heen weglekt. De belangrijkste taak van beleggers (en risicomanagers) is het voorkomen van een te grote beweeglijkheid, en dan vooral de negatieve beweeglijkheid, ofwel de grote uitschieters naar beneden. Regelmatig 40% verlies, ook al staan daar even zovele grote winsten van 50% tegenover, is uiteindelijk einde verhaal.
Spreiding is niet voor niets de belangrijkste les van beleggen. Als je een jaar van plus 10% afwisselt met een jaar van 0%, of plus 20% met min 10% (beide een gemiddelde van 5%) kom je wel positief en (veel) hoger uit. Als het even kan, wordt er nog een beleggingsstrategie ingebouwd, waarbij geprofiteerd wordt als zich een staartrisico voordoet. Wat dat betreft staat een andere boodschap van de Moderne Portefeuille Theorie, namelijk ‘diversificatie is de enige free lunch’, nog wél als een paal boven water.
Leverage, of ‘beleggen met een hefboom’, moet dan ook met de nodige voorzichtigheid worden bekeken. Leverage vergroot namelijk de volatiliteit en dus de volatility drag. Daarnaast is de belegger met leverage ook nog eens afhankelijk van de financier. Die kan de leverageregels veranderen (‘rien ne va plus’, het geld is niet meer van u).
Niet toevallig blazen hedge funds of banken (die ook leverage gebruiken: een euro spaargeld ophalen en tien uitlenen) zich bij tijd en wijle op. Brokers die hun klanten veel leverage toestaan - denk nog even terug aan Robinhood met GameStop - zijn ook niet veilig als de zwarte zwaan weer een keer voorbij vliegt.
Dit artikel bevat een persoonlijke mening van Harry Geels
